what is a technique for moving from the problem to the solution? judaism

Earlier getting started, let's talk near what the Tower of Hanoi problem is. Well, this is a fun puzzle game where the objective is to move an entire stack of disks from the source position to another position. Three simple rules are followed:

1. Only one disk can be moved at a time.
2. Each movement consists of taking the upper disk from ane of the stacks and placing it on peak of another stack. In other words, a disk can only exist moved if information technology is the uppermost disk on a stack.
3. No larger disk may be placed on top of a smaller disk.

Now, let's attempt to imagine a scenario. Suppose we have a stack of iii disks. Our task is to move this stack from source A to destination C. How do nosotros practice this?

Before we tin get there, let's imagine there is an intermediate point B.

3 disks.

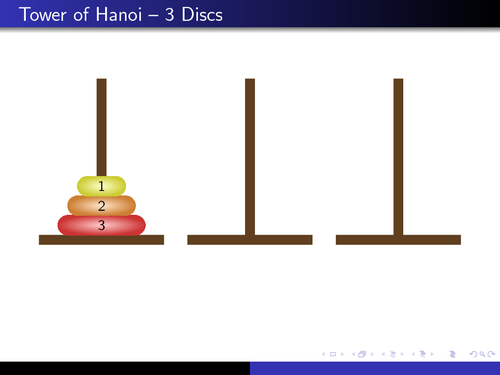
We tin utilize B as a helper to finish this job. Nosotros are now ready to move on. Let's go through each of the steps:

1. Move the showtime disk from A to C
2. Motility the first disk from A to B
3. Move the starting time disk from C to B
4. Motion the start disk from A to C
5. Move the first disk from B to A
6. Motility the first disk from B to C
7. Motion the first disk from A to C

Boom! We take solved our problem.

Tower of Hanoi for 3 disks. Wikipedia

You can see the animated prototype higher up for a better understanding.

Now, permit's try to build the algorithm to solve the trouble. Wait, we have a new discussion here: "Algorithm". What is that? Any idea? No problem, permit's run across.

Photo past bruce mars on Unsplash

What is an algorithm?

An algorithm is one of the nigh of import concepts for a software developer. In fact, I think it's not just of import for software development or programming, but for everyone. Algorithms bear on us in our everyday life. Let's see how.

Suppose you work in an role. So every morning y'all do a series of tasks in a sequence: beginning you wake up, then you go to the washroom, consume breakfast, get prepared for the office, leave home, then you lot may have a taxi or bus or start walking towards the office and, after a sure time, you reach your office. You can say all those steps grade an algorithm.

In simple terms, an algorithm is a set of tasks. I hope you haven't forgotten those steps we did to motility 3 disk stack from A to C. You tin can also say that those steps are the algorithm to solve the Belfry of Hanoi problem.

In mathematics and computer science, an algorithm is an unambiguous specification of how to solve a class of problems. Algorithms tin perform adding, data processing and automatic reasoning tasks. — Wikipedia

If you take a wait at those steps you can run into that we were doing the aforementioned chore multiple times — moving disks from ane stack to another. Nosotros tin telephone call these steps inside steps recursion.

Recursion

Recursion — giphy

Recursion is calling the same action from that action. Just like the above picture show.

So there is one rule for doing whatever recursive work: at that place must be a condition to finish that activity executing. I promise you understand the basics about recursion.

Now, let's try to build a procedure which helps u.s.a. to solve the Tower of Hanoi problem. We are trying to build the solution using pseudocode. Pseudocode is a method of writing out reckoner code using the English language.

                tower(disk, source, intermediate, destination) {  }              

This is the skeleton of our solution. We take the total disks number as an argument. Then we need to pass source, intermediate identify, and the destination so that we can sympathise the map which we will use to consummate the job.

Now we demand to find a terminal state. The terminal country is the state where we are non going to call this role anymore.

                IF deejay is equal 1              

In our case, this would be our final state. Because when there will be one disk in our stack then it is easy to but do that terminal stride and later on that our task will exist done. Don't worry if information technology's not clear to you. When nosotros achieve the cease, this concept will be clearer.

Alright, we have found our terminal state point where we move our deejay to the destination like this:

                move disk from source to destination              

Now nosotros call our function again by passing these arguments. In that case, nosotros dissever the stack of disks in two parts. The largest disk (nth disk) is in 1 part and all other (n-1) disks are in the 2d part. At that place nosotros call the method two times for -(north-1).

                belfry(disk - i, source, destination, intermediate)              

Equally we said we pass total_disks_on_stack — 1 as an argument. And and so once more we motility our deejay like this:

                move disk from source to destination              

Later on that we again call our method like this:

                belfry(disk - i, intermediate, source, destination)              

Let's meet our full pseudocode:

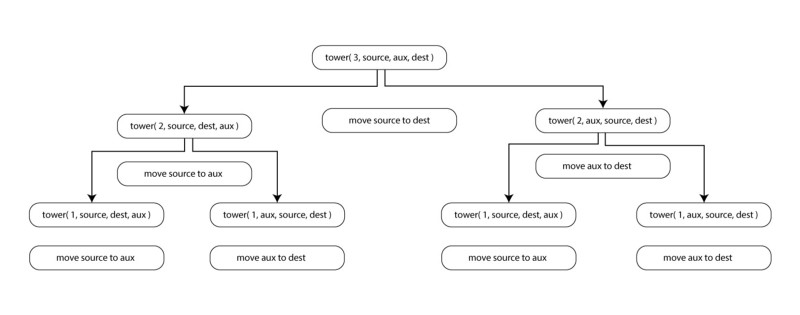
                tower(deejay, source, inter, dest)  IF disk is equal ane, So       movement disk from source to destination    ELSE       tower(deejay - ane, source, destination, intermediate)   // Footstep ane       move disk from source to destination                 // Step two       tower(disk - ane, intermediate, source, destination)   // Step 3    Finish IF     END              

This is the tree for three disks:

Tree of tower of hanoi (iii disks)

This is the total lawmaking in Ruby:

                def tower(disk_numbers, source, auxilary, destination)   if disk_numbers == i     puts "#{source} -> #{destination}"     return   end   tower(disk_numbers - one, source, destination, auxilary)   puts "#{source} -> #{destination}"   tower(disk_numbers - 1, auxilary, source, destination)   nil end              

Call tower(3, 'source','aux','dest')

Output:

                source -> dest source -> aux dest -> aux source -> dest aux -> source aux -> dest source -> dest              

Information technology took vii steps for three disks to achieve the destination. We call this a recursive method.

Photograph by Aron Visuals on Unsplash

Time complexity and space complication calculations

Time complexity

When we run code or an application in our machine information technology takes time — CPU cycles. But it's not the same for every reckoner. For instance, the processing time for a core i7 and a dual core are not the same. To solve this problem in that location is a concept used in computer science called time complication.

Fourth dimension complexity is a concept in estimator science that deals with the quantification of the corporeality of time taken by a fix of code or algorithm to procedure or run every bit a function of the amount of input.

In other words, time complexity is essentially efficiency, or how long a program function takes to process a given input. — techopedia

The time complication of algorithms is most commonly expressed using big O notation. It's an asymptotic note to represent the time complexity.

Now, the time required to move n disks is T(n). There are two recursive calls for (northward-1). There is ane abiding fourth dimension operation to motility a disk from source to the destination, let this be m1. Therefore:

                T(n) = 2T(north-i) + m1    ..... eq(i)              

And

                T(0) = m2, a constant   ...... eq(two) From eq (one) T(ane) = 2T(ane-ane) + m1      = 2T(0)+m1      = 2m2 + m1 ..... eq(3) [From eq 2] T(2) = 2T(2-1) + m1      = 2T(1) + m1      = 4m2 + 2m1 + m1 .... eq(4) [From eq(three)] T(3) = 2T(3-1) + m1      = 2T(2) + m1      = 8m2 + 4m1 + 2m1 + m1  [From eq(four)]              

From these patterns — eq(ii) to the final one — we can say that the fourth dimension complexity of this algorithm is O(2^n) or O(a^n) where a is a constant greater than 1. And so it has exponential time complexity. For the single increase in problem size, the time required is double the previous one. This is computationally very expensive. Almost of the recursive programs have exponential time, and that is why it is very difficult to write them iteratively.

Space complexity

After the explanation of time complexity analysis, I call back you tin can guess at present what this is…This is the calculation of space required in ram for running a lawmaking or application.

In our instance, the space for the parameter for each call is independent of northward, significant it is constant. Let information technology be J. When we do the 2d recursive call, the first one is over. That means that nosotros can reuse the space after finishing the first i. Hence:

                T(n) = T(n-ane) + one thousand .... eq(one) T(0) = one thousand, [constant] .... eq(two) T(1) = T(i-1) + k      = T(0) + k      = 2K T(two) = 3k T(3) = 4k              

Then the space complexity is O(n).

After these analyses, we tin can see that time complexity of this algorithm is exponential only space complexity is linear.

Conclusion

From this article, I promise you can now understand the Tower of Hanoi puzzle and how to solve it. Too, I tried to give you some basic understanding about algorithms, their importance, recursion, pseudocode, time complexity, and infinite complexity. If you want to learn these topics in item, here are some well-known online courses links:

1. Algorithms, Part I
2. Algorithms, Part Ii
3. The Google form on Udacity
4. Javascript Algorithms And Information Structures Certification (300 hours)

Y'all tin visit my data structures and algorithms repo to see my other issues solutions.

I am on GitHub | Twitter | LinkedIn

---

---

Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

lanedents1968.blogspot.com

Source: https://www.freecodecamp.org/news/analyzing-the-algorithm-to-solve-the-tower-of-hanoi-problem-686685f032e3/

Share this post